Encoding EAN 13:

Cette page en Français

An EAN-13 barcode has the following physical structure:

• Left guard bars, or start sentinel, encoded as 101.
• The second character of the number system code, encoded as described below.
• The five characters of the Manufacturer Code, encoded as described below.
• Center guard pattern, encoded as 01010
• The five characters of the product code, encoded as right-hand characters, described below.
• Check digit, encoded as a right-hand character, described below.
• Right guard bars, or end sentinel, encoded as 101.
  

The characters that are encoded to the left of the center guard pattern are considered the "left hand side" of the symbol whereas all characters encoded to the right of the center guard pattern are considered the "right hand side" of the symbol.

The first character of the EAN-13 number system code (i.e., the first digit of the EAN-13 value) is encoded in the parity of the characters of the left-hand side of the symbol. That is to say, the value of the first character of the EAN-13 value determines the parity with which each of the characters in the left-hand side of the barcode will be encoded from the following table.

EAN Character Set Encoding Table:

This table indicates how to encode each digit of an EAN-13 barcode depending on which half (left or right) of the barcode the digit is found in. In the case of a left-hand digit, the encoding (odd or even parity) is based on the value of the first digit of the number system code (see parity encoding table below).

Digit	Left-Hand Encoding		Right-Hand Encoding
	Odd Parity (Set A)	Even Parity (Set B)	Set C
0	0001101	0100111	1110010
1	0011001	0110011	1100110
2	0010011	0011011	1101100
3	0111101	0100001	1000010
4	0100011	0011101	1011100
5	0110001	0111001	1001110
6	0101111	0000101	1010000
7	0111011	0010001	1000100
8	0110111	0001001	1001000
9	0001011	0010111	1110100

NOTE: For "left-hand encoding", odd and even parity is often 
referred to as "character set A" (odd) and "character set B" (even).

Observations:

• An EAN-13 character is represented in 7 elements consisting of 2 bars and 2 spaces. 
  No bar or space may be longer than 4 elements. The only exception to this rule is the left and right guard bars (3 elements each) and the center guard bar (5 elements long).
   
• All characters in the left-hand side of the barcode always start with a 0 (space) while all characters in the right-hand side of the barcode always start with a 1 (bar).
   
• The "right-hand" encoding pattern is exactly the same as the "left-hand odd" encoding pattern, but with 1's changed to 0's, and 0's changed to 1's.
   
• The "left-hand even" encoding pattern is based on the "left-hand odd" encoding pattern. To arrive at the even encoding, work from the left encoding and do the following: 
  1) Change all the 1's to 0's and 0's to 1.;
  2) Read the resulting encoding in reverse order (from right to left).
  The result is the "left-hand even" encoding pattern.

EAN Parity Encoding Table:

The following table indicates the parity with which each character in the left-hand side of the barcode should be encoded.

The parity is based on the first digit of the EAN-13 value.

For example, our EAN-13 is 761234567890.
In this case, the first digit of the number system code is the first digit 7 , so the parity would be based on the number 7 in the following table:

1st Number System Digit	Parity to encode with
	2nd Number System Digit	Manufacturer Code Characters
		1	2	3	4	5
0 (UPC-A)	Odd	Odd	Odd	Odd	Odd	Odd
1	Odd	Odd	Even	Odd	Even	Even
2	Odd	Odd	Even	Even	Odd	Even
3	Odd	Odd	Even	Even	Even	Odd
4	Odd	Even	Odd	Odd	Even	Even
5	Odd	Even	Even	Odd	Odd	Even
6	Odd	Even	Even	Even	Odd	Odd
7	Odd	Even	Odd	Even	Odd	Even
8	Odd	Even	Odd	Even	Even	Odd
9	Odd	Even	Even	Odd	Even	Odd

Observation:

• The second number system digit is always encoded with odd parity.
• A UPC-A barcode always has a first number system digit of zero, and therefore uses exclusively odd parity.
  In fact, any EAN-13 symbol which has a first number system digit of 0 is actually an UPC-A symbol, not an EAN-13 symbol.
• All EAN-13 symbols (that have a first number system digit that is non-zero) always have three left-hand characters that are encoded using even parity and two that are encoded using odd parity.

Encoding Example:

This example will encode the EAN-13 barcode which represents the value:

7612345678900

• Number System 76,
• Manufacturer Code 12345,
• Product Code 67890,
• Check Digit is 0.

The first digit of the number system is 7.

Consulting the parity encoding table for the digit 7, we find that the parity for the second number system digit and the manufacturer code should follow the pattern:

Odd Even Odd Even Odd Even.

That means:

• the second number system digit will be encoded from the left-hand odd parity table,
• the first digit of the manufacturer code will be encoded with left-hand even parity, etc.

We can now start encoding our barcode with the following steps:

Digit name	Numeric Value	Encoded with	Binary
Left Guard	-	-	101
2nd Number System	6	Odd	0101111
1st Manufacturer	1	Even	0110011
2nd Manufacturer	2	Odd	0010011
3rd Manufacturer	3	Even	0100001
4th Manufacturer	4	Odd	0100011
5th Manufacturer	5	Even	0111001
Central Guard	-	-	01010
1st Product Code	6	C	1010000
2nd Product Code	7	C	1000100
3rd Product Code	8	C	1001000
4th Product Code	9	C	1110100
5th Product Code	0	C	1110010
Check Digit	0	C	1110010
Right Guard	-	-	101

The barcode is then constructed by simply concatenating all the strings together.

10101011110110011001001101000010100011011100101010101000010001001001000111010011100101110010101

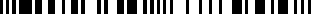
1 represents a bar and 0 represents a space.

Thus if we convert this string of numbers to their graphical representation we end up with the following barcode:

Informations Gomaro s.a.